The EQC-EDA Method
We are developing a framework for analyzing electronic structure in atoms, molecules and in extended structures. The uniqueness of the energy partitioning at the core of this framework (shown below) is that it can be interchangeably applied to analyze total energies and energy processes using either quantum chemical output (wave functions) or, in principle, experimental data (XPS and UPS spectra, thermochemistry, X-ray structures). As such, the methodology holds the potential for bridging scientific disciplines, and it constitutes the first step toward an experiential quantum chemistry.
A video lecture describing some of the basics of this methodology can be found here.
Try It On Your Chemistry
We have made an easy-to-use python script that parses output from popular quantum chemistry codes, such as Gaussian and ORCA. You can use it to analyze a given electronic structure (A), a transformation (A → B), or a bond formation (A + B → C).
Download the latest version of the script here.
Background Theory
Energy Partitioning:
The total energy can be decomposed as:
 ,
,
where n is the number of electrons and E, or ΔE, can be calculated at any quantum chemical level of theory [36]. Experimentally, E equals the sum of all adiabatic ionization potentials of consecutive ions, and ΔE can be approximated from thermochemistry (heats of reaction/formation corrected for vibrational effects).
χ ̅ is the average electron energy, or, within Koopman’s theorem, the average binding energy. Conceptually, this term can be attributed to electronegativity, covalence, and orbital stabilization/destabilization. Computationally, χ ̅ is most straightforwardly approximated as the average eigenvalue of all occupied levels. Experimentally, it can be estimated using X-ray photoelectron spectroscopy (XPS) and ultraviolet photoelectron spectroscopy (UPS) for all single ionizations.
VNN is the nuclear-nuclear repulsion. It is a direct consequence of the molecular structure, and can be calculated quantum mechanically, or be obtained using X-ray or microwave structure determination.
Eee quantifies the average multi-electron interaction energy, and can be indirectly obtained from knowing the other terms of the equation. Provided that the electron density can be obtained with sufficient accuracy, Eee may be decomposed further, separating out the classical electron-electron Coulomb repulsion and all remaining non-classical interactions such that Eee = EC + EQ.
Q, A Descriptor for Distinguishing Chemical Bonds:
Q is condensation of the above summarized energy partitioning [37]. It is defined so to weigh the relative importance of a first term related to covalency, electronegativity or average orbital stabilization, with a second term associated with electron-electron interactions, or charge drift.
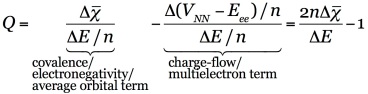
The Q scale is unbound and unit less, and can take both positive and negative values. On the positive side of the scale, Q ranges from Q=1, attributed to ‘perfect covalency’, where orbital stabilization perfectly describes the energy change, to Q>1, where disfavoring electron-electron interactions become more significant, to Q>>1, where dispersion and strong electrostatic interactions fall. On the negative side, Q=–1 is associated with ‘perfect ionicity’, where the energy change is driven by electron-electron interactions and the orbital term equals zero, Q<–1 corresponds to polar, ionic and metallogenic bonds, where repulsive orbital interactions play an increasingly important role.
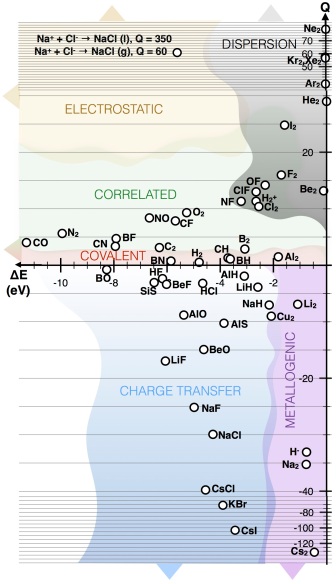
The Q-descriptor applied to diatomic bonds illustrates its predictive potential, and suggest a utility for using small model systems to infer properties of condensed phase materials. Reproduced from J. Am. Chem. Soc., 138, 3731-3744, 2016.
Key References
Toward an Experimental Quantum Chemistry: Exploring a New Energy Partitioning
M. Rahm, R. Hoffmann
J. Am. Chem. Soc., 137, 10282–10291, 2015
Distinguishing Bonds
M. Rahm, R. Hoffmann
J. Am. Chem. Soc., 138, 3731-3744, 2016
Electronegativity Seen as the Ground State Average Valence Electron Binding Energy
M. Rahm, T. Zeng, R. Hoffmann
J. Am. Chem. Soc, 141,342-351, 2019
Squeezing all Elements in the Periodic Table: Electron Configuration and Electronegativity of the Atoms under Compression
M. Rahm, R. Cammi, N. W. Ashcroft, R. Hoffmann
J. Am. Chem. Soc., DOI: 10.10121/jacs.9b02634, 2019
Applications (by us and others):
CF2H, a Hydrogen Bond Donor
C. D. Sessler, M. Rahm, S. Becker, J. M. Goldberg, F. Wang, S. J. Lippard
J. Am. Chem. Soc. 139, 9325-9332, 2017
A Variety of Bond Analysis Methods, One Answer? An Investigation of the Element-Oxygen Bond of Hydroxides HnXOH.
M. Fugel, J. Beckmann, D. Jayatilaka, G. V. Gibbs, S. Grabowsky
Chem. – Eur. J. 24, 6248-6261, 2018